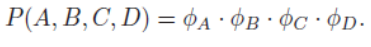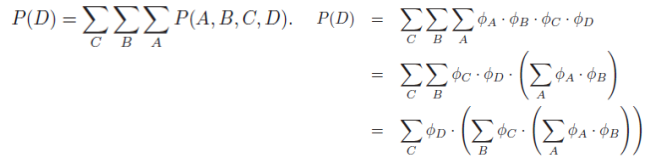Variable Elimination Basics
Dynamic programming techniques can be used to perform inference even for certain large and complex networks in a very reasonable time.
Considering the inference task in a very simple network
A → B → C → D
We first provide a phased computation, which uses results from the previous phase for the computation in the next phase.
We then reformulate this process in terms of a global computation on the joint distribution.
Dynamic programming techniques can be used to perform inference even for certain large and complex networks in a very reasonable time.
Considering the inference task in a very simple network A → B →C → D. We first provide a phased computation, which uses results from the previous phase for the computation in the next phase.
We then reformulate this process in terms of a global computation on the joint distribution.
Assume that our first goal is to compute the probability P(B), that is, the distribution
over values b of B. Basic probabilistic reasoning (with no assumptions) gives
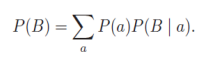
Each number P(a) is in the CPD for A, and each number P(b | a) is in the CPD for B.
If A has k values and B has m values, the number of basic arithmetic operations
required is O(k x m): to compute P(b), we must multiply P(b | a) with P(a) for each of
the k values of A, and then add them up, that is, k multiplications and k - 1 additions;
This process must be repeated for each of the m values b.
Similarly for C , we have
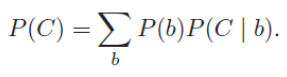
Similarly P(D) can be computed.
Consider the process of generating the entire joint and summing it out, which
requires that we generate k^n probabilities for the different events x1,..., xn.By the chain rule for Bayesian networks, the joint P(A,B,C,D) decomposes as -
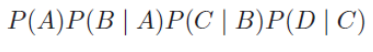
To compute P(D), we need to sum together all of the entries where D = d^1 and to (separately) sum together all of the entries where D = d^2. The exact computation that needs to be performed, for binary-valued variables A,B,C,D is
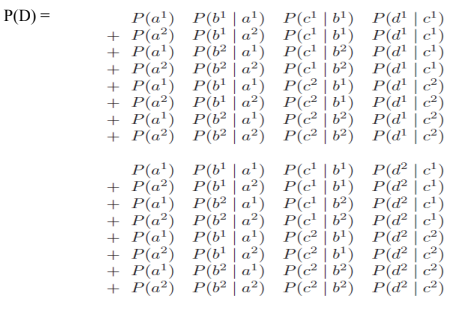Repeated terms can gain significant computational savings by computing terms once and storing them.
This procedure is said to be performing dynamic programming.
